philokatholos

Είναι ευρέως γνωστό πως εκτός από την μυστηριώδη προσωπική σχέση που είχε ο αυτοδίδακτος Ραμανουτζάν με τους αριθμούς, είχε και μία ασυναγώνιστη ικανότητα για ταχύτατους υπολογισμούς. Χαρακτηριστικό παράδειγμα είναι η συνάντηση που είχε με τον Χάρντι, όταν ο τελευταίος τον επισκέφθηκε στο νοσοκομείο: προκειμένου να τον διασκεδάσει του ανέφερε πως το ταξί με το οποίο κατέφθασε στο νοσοκομείο είχε έναν πολύ βαρετό αριθμό, το $1729$. Ο Ραμανουτζάν γρήγορα τον διόρθωσε λέγοντας:

“Όχι, όχι, ο αριθμός αυτός έχει πολύ μεγάλο ενδιαφέρον καθώς είναι ο μικρότερος αριθμός ο οποίος δύναται να γραφτεί ως άθροισμα δύο κύβων με δύο διαφορετικούς τρόπους: $1729 = 1^3 + 12^3 = 9^3 + 10^3$”

Αριθμοί με ανάλογες ιδιότητες καλούνται σήμερα “αριθμοί των ταξί” λόγω αυτού του περιστατικού. Εκ πρώτης όψεως, ίσως φαίνεται υπερβολή να μελετήσει κάποιος τέτοιους αριθμούς περαιτέρω. Όπως όμως συμβαίνει συχνά στην Θεωρία Αριθμών, φαινομενικά απλές ιδιότητες φανερώνουν πολύ βαθιές αλγεβρο-γεωμετρικές δομές στο μαθηματικό σύμπαν. Πράγματι, τα τελευταία χρόνια οι αριθμοί αυτοί του Ραμανουτζάν βρίσκουν απρόσμενες εφαρμογές στις ιδιότητες των μελανών οπών και μας οδηγούν σε μια καλύτερη κατανόηση της φυσικής τους κοντά στον ορίζοντα γεγονότων ή στο λεγόμενο παράδοξο της πληροφορίας. Αλλά και οι υπόλοιπες εργασίες του Ραμανουτζάν φαίνεται να σχετίζονται με την κβαντική βαρύτητα, όπως για παράδειγμα τις επιφάνειες $K3$ που αποτελούν χαμηλότερης διάστασης ανάλογα των συμπαγοποιήσεων των εξωτικών διαστάσεων στη θεωρία χορδών και την κβαντική βαρύτητα.

Ένα παρόμοιο περιστατικό συνέβη ένα μεσημέρι στο σπίτι που μοιραζόταν με τον Ινδό ομογενή του και μετέπειτα διάσημο στατιστικολόγο Μαχαλανόμπις, την ώρα που ο Ραμανουτζάν βρισκόταν στην κουζίνα και μαγείρευε. Ο Μαχαλανόμπις του είπε πως διάβασε έναν γρίφο στην Βρετανική εφημερίδα Strand ο οποίος τον προβλημάτησε και είχε ως εξής:

Βρισκόμαστε σε μια οδό στην πόλη Λέβεν του Βελγίου στην οποία $n$ σπίτια είναι αριθμημένα με την σειρά $1, 2, 3, \dots, n$. Υπάρχει ένα σπίτι για το οποίο το άθροισμα των σπιτιών αριστερά του είναι το ίδιο με το άθροισμα των σπιτιών δεξιά του. Εάν το πλήθος των σπιτιών $n$ είναι ένας αριθμός μεταξύ του $50$ και του $500$, μπορείτε να βρείτε τι νούμερο έχει αυτό το μοναδικό σπίτι;

Ο Ραμανουτζάν σκέφτηκε για λίγα μόνο δευτερόλεπτα και έδωσε στιγμιαία την απάντηση. Ο Μαχαλανόμπις κατάπληκτος τον ρώτησε πως κατάφερε να βρει τη σωστή απάντηση τόσο γρήγορα και ο Ραμανουτζάν απάντησε:

«Είναι απλό. Όταν άκουσα το πρόβλημα, ήξερα πως η απάντηση θα είναι ένα συνεχές κλάσμα. Τότε αναρωτήθηκα: όμως ποιο συνεχές κλάσμα; Και τότε η απάντηση μου ήρθε στο μυαλό».

Το πρόβλημα μοιάζει απλό αλλά δεν είναι τόσο στοιχειώδες έτσι ώστε να μπορεί να επιλυθεί τόσο γρήγορα από οποιονδήποτε δυνατό λύτη. Αλλά πέρα από αυτό, η απάντηση του Ραμανουτζάν είναι ακόμα πιο ενδιαφέρουσα και σε ένα δεύτερο επίπεδο. Θυμηθείτε πως το πρόβλημα είναι διατυπωμένο με τέτοιο τρόπο έτσι ώστε να περιορίζει το εύρος των δυνατών λύσεων, καθώς περιορίζει το πλήθος των σπιτιών σε $50-500$. Ο Ραμανουτζάν βρίσκοντας ένα συνεχές κλάσμα ως απάντηση, στην πραγματικότητα αντί να βρει μία λύση στο πρόβλημα, βρίσκει όλες τις δυνατές λύσεις ταυτόχρονα! Στην παρούσα ανάρτηση θα ήθελα να προσπαθήσω να εξηγήσω πως μπορεί να φτάσει κανείς σε αυτή την γενικευμένη λύση. Τι είναι όμως ένα συνεχές κλάσμα;

Ένα συνεχές κλάσμα είναι μια μαθηματική έκφραση αποτελούμενη από μια επαναλαμβανόμενη διαδικασία ως εξής:

Παρατηρήστε πως αν αυτή η διαδικασία τελικά περατώνεται, τότε ο αριθμός του αποτελέσματος θα είναι υποχρεωτικά ρητός, ενώ αν όχι, ο αριθμός αυτός θα είναι εξ’ορισμού άρρητος (θυμηθείτε πως άρρητος είναι κάθε αριθμός που δεν είναι ρητός, δηλαδή κάθε αριθμός που δεν δύναται να γραφτεί ως λόγος δύο άλλων ακεραίων). Η ιστορία έχει ως εξής: η μυστικιστική σχολή των Πυθαγορείων δίδασκε πως κάθε αριθμός δύναται να γραφτεί ως ο λόγος δύο άλλων φυσικών αριθμών. Το δόγμα αυτό δεν ήταν αφηρημένο: σχετιζόταν με την γενικότερη φιλοσοφία και κοσμοθέαση που είχαν οι Πυθαγόρειοι σχετικά με την μουσική των ουρανίων σφαιρών, τη γεωμετρία, την ιερά τετρακτύ, την δωδεκαεδρική δομή του κόσμου, την πεμπτουσία και φυσικά το ίδιο το Πυθαγόρειο θεώρημα: $c^2 = a^2 + b^2$. Η ύπαρξη αρμονικών σχέσεων όπως $5^2 = 3^2 + 4^2$ που καλούνται Πυθαγόρειες τριάδες, ήταν αρκετές για να τους πείσουν για την μαθηματική κατανοησιμότητα του Σύμπαντος.

Μία ανεκδοτολική ιστορία λέει πως ένα ηλιόλουστο πρωϊνό όπου μια ομάδα μαθητών ταξίδευε προς την σχολή στον Κρότωνα, ο Ίππασος ο Μεταπόντιος είχε χαράξει στην κουπαστή με το ξίφος του ένα τετράγωνο με πλευρά ίση με $1$ και αναρωτιόταν ποιο είναι το μήκος της διαγωνίου σύμφωνα με το Πυθαγόρειο θεώρημα. Με άλλα λόγια, ποιος είναι εκείνος ο αριθμός που όταν τον πολλαπλασιάσω με τον εαυτό του να μου δώσει αποτέλεσμα $2$; Φανερά μπερδεμένος, φώναξε τον ίδιο τον Πυθαγόρα προκειμένου να του δείξει την κατασκευή και να τον βοηθήσει αλλά η παράδοση θέλει τον Πυθαγόρα να σκοτώνει (ή σε ευνοϊκότερα σενάρια να πετάει στη θάλασσα) τον Ίππασο μόλις αντιλήφθηκε σιωπηρά πως η θεωρία του δεν μπορεί να ευσταθεί.

Πράγματι λοιπόν, δεν υπάρχουν αριθμοί $p$ και $q$ έτσι ώστε $\frac{p^2}{q^2} =2$, το $\sqrt{2}$ είναι με άλλα λόγια, άρρητος. Σε αντίθεση με τους ρητούς αριθμούς, που είτε το δεκαδικό ανάπτυγμα τελειώνει (όπως το $\frac{1}{2}=0.5$) είτε είναι άπειρο αλλά επαναλαμβάνεται (όπως το $\frac{1}{3}=0.333…$), τα δεκαδικά ψηφία ενός άρρητου αριθμού δεν τελειώνουν ποτέ και μάλιστα η κατανομή των ψηφίων που ακολουθούν είναι “χαοτική” και ποτέ επαναλαμβανόμενη π.χ $\sqrt{2} = 1.41421356237…$. Αφού λοιπόν δεν μπορούμε να εκφράσουμε έναν άρρητο αριθμό, τίθεται με φυσικό τρόπο το ερώτημα πως μπορούμε τουλάχιστον να τον προσεγγίσουμε με μία ικανοποιητική προσέγγιση. Η έννοια των συνεχών κλασμάτων του Ραμανουτζάν προσφέρουν πράγματι μια τέτοια δυνατότητα. Για παράδειγμα γράφοντας το $\sqrt{2}$ ως $\sqrt{2} = 1 + (\sqrt{2} -1)$ και παρατηρώντας ότι: $(\sqrt{2} – 1)(\sqrt{2}+1) = 1$ μπορούμε να γράψουμε το $\sqrt{2}$ αναδρομικά:

$\begin{align} \sqrt{2} &= 1+\frac{1}{1+\sqrt{2}} \\ &=1 + \frac{1}{2+\frac{1}{1+\sqrt{2}}} \\ &=1 + \frac{1}{2+\frac{1}{2+\frac{1}{1+\sqrt{2}}}} \\ &=1 + \frac{1}{2+\frac{1}{2+\frac{1}{2+\ldots }}} \end{align}$

η χρησιμοποιώντας ακόμα πιο οικονομική γραφή: $\sqrt{2} = [1; \bar{2}]$.

Το πρόβλημα των προσεγγίσεων των αρρήτων είχε ήδη απασχολήσει τους αρχαίους Έλληνες και φυσικά συνέχιζε να προβληματίζει και τους ανατολικούς Ρωμαίους όπως φαίνεται από την βαθιά μεταφυσική αρχιτεκτονική της Αγίας Σοφίας όπου κατά την τριχοτόμηση του Αριστοτέλη “τρεῖς ἂν εἶεν φιλοσοφίαι θεωρητικαί͵ μαθηματική͵ φυσική͵ θεολογική”, αντανακλά γνώση τόσο του προσεγγιστικού λόγου $\frac{22}{7}$ για τον αριθμό $\pi$ όπως χρησιμοποιήθηκε από την εξαντλητική μέθοδο του Αρχιμήδη αλλά και των μετέπειτα θεωριών του Ήρωνα του Αλεξανδρέα για το $\sqrt(2)$. Οι λόγοι αυτοί κατά κάποιο τρόπο επιλύουν το πρόβλημα μηχανικής που δημιουργείται από ένα αποδεδειγμένα αδύνατο μαθηματικό πρόβλημα όπως είναι ο τετραγωνισμός του κύκλου και κατ’αναλογία το αρχιτεκτονικό αποτύπωμα δίνει μια αίσθηση του αρρήτου του Θεού Λόγου και του μέγα μυστηρίου της Ενσαρκώσεως που υπερβαίνει πάσα φύση και πάσα έννοια.

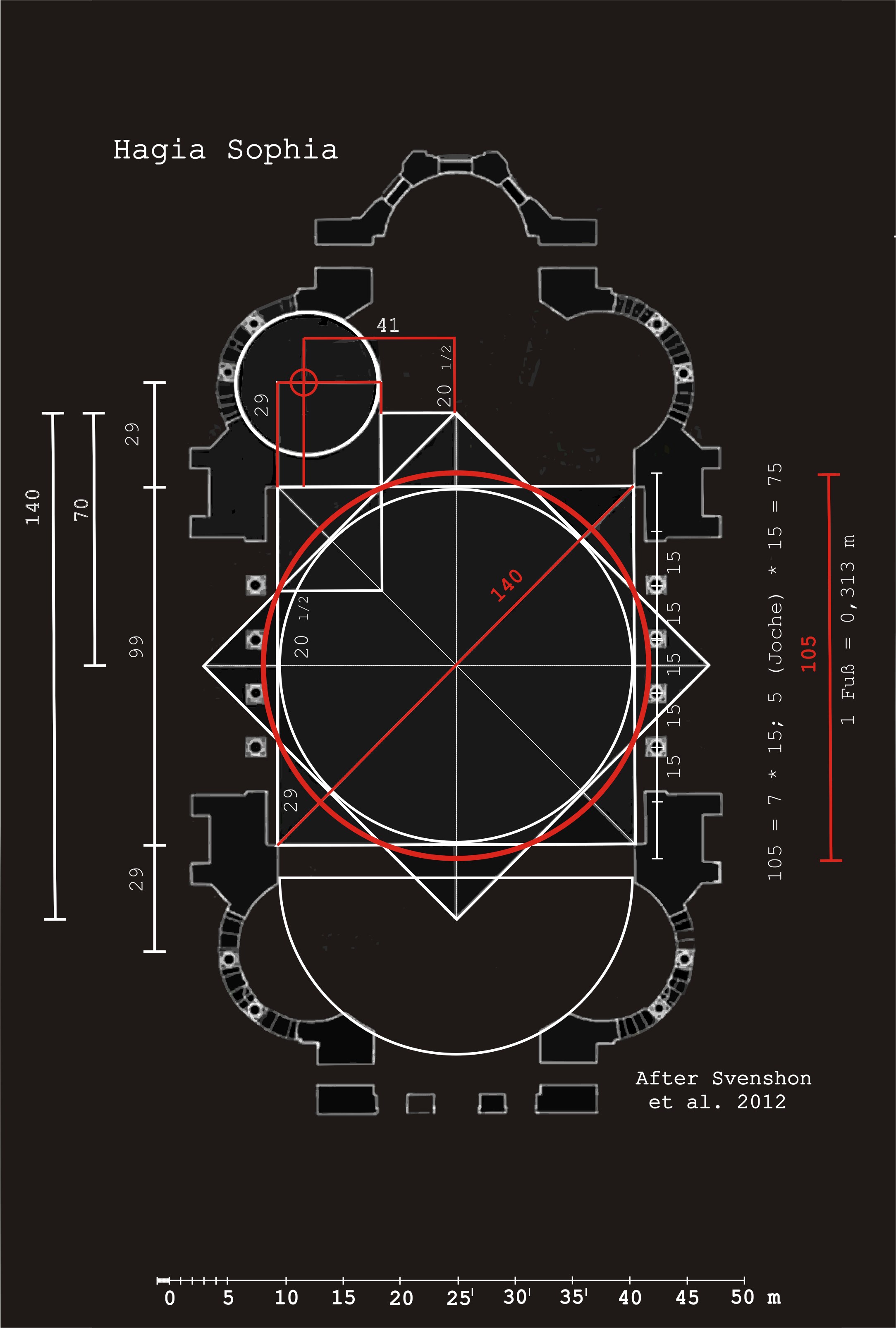
Έτσι, με σημερινούς όρους θα λέγαμε πως οι αρχαίοι Έλληνες υπολόγισαν διαδοχικές προσεγγίσεις, ολοένα μεγαλύτερης ακρίβειας, μέσω ενός συνεχούς κλάσματος για το $\sqrt{2}$, για παράδειγμα: $1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \frac{99}{70},\frac{239}{169},\frac{577}{408}$ κ.ο.κ. Πράγματι, αυτή η ακολουθία δίνει μια προσεγγιστική απάντηση για το μήκος της υποτείνουσας στο πρόβλημα του Ίππασου που αναφέρθηκε πιο πάνω.

Ας δούμε όμως τώρα τι σχέση έχουν όλα αυτά με τη λύση του Ραμανουτζάν. Έστω ότι υπάρχουν $n$ σπίτια και το σπίτι που αναζητούμε είναι το $z$. Δηλαδή,

$$1,2,3,\dots,z,z+1,z+2,\dots,…,n$$

Θέλουμε το άθροισμα αριστερά του $z$ να είναι το ίδιο με το άθροισμα δεξιά του, επομένως:

$$1+2+3+\dots+(z-1) = (z+1) + (z+2) + (z+3) + \dots + n$$

Άρα, από τον τύπο άθροισης για αριθμητικές προόδους θα έχουμε ότι:

$$\frac{z(z-1)}{2} = \frac{n(n+1)}{2} – \frac{z(z+1)}{2}$$

Δηλαδή,

$$z(z-1) = n(n+1) – z(z+1)$$.

Κάνοντας τις πράξεις, βρίσκουμε ισοδύναμα ότι:

$$8z^2 = (2n+1)^2 -1$$

Οπότε, θέτοντας $x=2n+1$ και $y=2z$ καταλήγουμε στην εξίσωση $x^2 – 2 y^2 = 1$ η οποία είναι γνωστή με το όνομα ενός άλλου Ινδού μαθηματικού που έζησε τον 7ο αιώνα, του Βραχμαγκούπτα. Σήμερα είναι γνωστή ως εξίσωση Pell και είναι υπεύθυνη για ολόκληρη την θεωρία των λεγόμενων πραγματικών τετραγωνικών επεκτάσεων $\mathbb{Q}(\sqrt{d})$. Αν αντικαταστήσουμε τις προσεγγίσεις που αναφέραμε πιο πάνω θα δούμε ότι η εξίσωση ικανοποιείται διαδοχικά:

$$3^2 – 2 \cdot 2^2 = 1$$

$$7^2 – 2 \cdot 5^2 = 1$$

$$17^2 – 2 \cdot 12^2 = 1$$

$$\dots$$

Επομένως, παίρνοντας για λύση της εξίσωσης Pell που μας ενδιαφέρει το συνεχές κλάσμα των διαδοχικών προσεγγίσεων του $\sqrt{2}$ θα έχουμε πράγματι ως λύσεις τα ζεύγη

$$(x,y): (3,2), (17,12), (99,70), (577,408), \dots$$

ενώ χρησιμοποιώντας τους αντίστροφους μετασχηματισμούς $n = \frac{x-1}{2}$ και $z = \frac{y}{2}$ τελικά παίρνουμε όλες τις δυνατές (άπειρες) λύσεις:

$$(n, z): (8, 6), (49, 35), (288, 204), \dots$$

Δεδομένου ότι η αρχική διατύπωση του προβλήματος περιείχε τον περιορισμό το $n$ να βρίσκεται μεταξύ $50-500$ η μόνη δυνατή απάντηση (η απάντηση που έδωσε ο Ραμανουτζάν στιγμιαία) είναι ότι το πλήθος των σπιτιών πρέπει να είναι συνολικά $288$ και το σπίτι έχει αριθμό $204$!

Πράγματι, μπορεί να ελέγξει κανείς ότι:

$$1+2+3+4+\dots+203 = 205+206+\dots+288 = 20706$$

Κατά παρόμοιο τρόπο, μπορεί κανείς να υπολογίσει την αμέσως επόμενη λύση, δηλαδή τον αριθμό του σπιτιού όταν το πλήθος των σπιτιών είναι μεγαλύτερο από $288$.

The boy in the front line is probably thinking: “As $10^2 + 11^2 + 12^2 = 365$ and $13^2 + 14^2 = 365$, therefore $\frac{10^2 + 11^2 + 12^2 + 13^2 + 14^2}{365} = \frac{2 \times 365}{365} = 2$”.

But why does the pupil behind, looks so scared while staring at him?

And what is he possibly trying to say to his teacher?

The Jacobi theta function is defined as $$\theta(z, \tau) = \sum_{n \in \mathbb{Z} } e^{\pi i n^2 \tau + 2 \pi i n z}$$ and it transforms under $\theta(z+1, \tau) = \theta(z, \tau)$ and $\theta(z, -\frac{1}{\tau}) = (-i \tau)^{\frac{1}{2}} e^{\pi i z^2 \frac{1}{\tau}} \theta(z, \tau)$. Because it has a unique root $z = \frac{1}{2} (z+1)$ up to periodicity, using Weierstrass factorization theorem we can write it as: $$\theta(z, \tau) = \prod_{n=1}^{\infty} (1-q^n)(1+wq^{n-\frac{1}{2}})(1+\frac{1}{w} q^{n-\frac{1}{2}} ) $$ where $w=e^{2 \pi i z}$ and $q = e^{2 \pi i \tau}$. We often need the asymptotic behavior of $\theta(z, \tau)$ as $q \rightarrow 0$ or as $q \rightarrow 1$. The former can be read immediately from either forms above, but the latter is not manifest in either of them, because an infinite number of terms contribute. It can be obtained from the modular transformation $\tau \rightarrow -\frac{1}{\tau}$, which relates the two limits by $q \rightarrow e^{\frac{2 \pi^2}{lnq}}$.

We can also define theta functions with characteristics as follows:

$$\Theta^{a}_{b}(z, \tau) := e^{\pi i a^2 \tau + 2 \pi i a (z+b)} \theta(z + a\tau + b, \tau)$$ $$= \sum_{n \in \mathbb{Z}} e^{\pi i (n+a)^2 \tau + 2 \pi i (n+a)(z+b)}$$. Then, we further define:

$$\theta_{00}(z, \tau) := \Theta^{0}_{0}(z, \tau) = \sum_{n \in \mathbb{Z}} q^{\frac{n^2}{2}} $$

$$\theta_{01}(z, \tau) := \ \Theta^{0}_{\frac{1}{2}} (z, \tau) = \sum_{n \in \mathbb{Z}} (-1)^n q^{\frac{n^2}{2}} z^n $$

$$\theta_{10}(z, \tau) := \Theta^{\frac{1}{2}}_{0} (z, \tau) = \sum_{n \in \mathbb{Z}} q^{(n-\frac{1}{2})^2} z^{n-\frac{1}{2}} $$

$$\theta_{11}(z, \tau) := \Theta^{\frac{1}{2}}_{\frac{1}{2}} (z, \tau) = -i \sum_{n \in \mathbb{Z}} (-1)^n q^{(n-\frac{1}{2})^2} z^{n-\frac{1}{2}} $$

Then, we have the following infinite product representations, respectively:

$$ \theta_{00}(z, \tau) = \prod_{n=1}^{\infty} (1-q^n) (1 + w q^{(n-\frac{1}{2})})(1+\frac{1}{w} q^{n-\frac{1}{2}})$$

$$ \theta_{01}(z, \tau) = \prod_{n=1}^{\infty} (1-q^n) (1 – w q^{(n-\frac{1}{2})})(1-\frac{1}{w} q^{n-\frac{1}{2}})$$

$$ \theta_{10}(z, \tau) = 2 e^{\frac{1}{4} \pi i \tau} cos(\pi z) \prod_{n=1}^{\infty} (1-q^n) (1 + w q^{n})(1+\frac{1}{w} q^{n})$$

$$ \theta_{11}(z, \tau) = -2 e^{\frac{1}{4} \pi i \tau} sin(\pi z) \prod_{n=1}^{\infty} (1-q^n) (1 – w q^{n})(1-\frac{1}{w} q^{n})$$

Now, we have the following identity, which is unique of its type:

Theorem (Jacobi, 1829): $$\theta_{00}(0, \tau)^4 – \theta_{01}(0, \tau)^4 – \theta_{10}(0, \tau)^4 = 0$$

or in other words, that:

$$\prod_{n=1}^{\infty} (1 + q^{2n-1})^8 – \prod_{n=1}^{\infty} (1-q^{2n-1})^8 = 16q \prod_{n=1}^{\infty}(1+q^{2n})^8$$

This identity can be seen as a special case of Riemann-Mumford relations (namely R5) as found in Mumford’s Tata lectures. The mathematical interpretation comes from the triality of $Spin(8)$. Jacobi himself, not realizing any of its immediate implications of this identity he referred to it as “aequatio identica satis abstrusa” (a very obscure equation). Some 150 years later, string theory provided a natural explanation for it, namely that, it is the requirement of spacetime supersymmetry at 1-loop order in string perturbation theory. More specifically, this remarkable, non-trivial mathematical identity implies that the full superstring vacuum amplitude vanishes, which provides very strong evidence in favor of spacetime supersymmetry of string theory in $d=10$. As we will see below, it simply reflects the fact that the spacetime N-S sector bosons and R-sector fermions contribute the same way in equal numbers (but with opposite signs due to spin statistics). Indeed, there is a physical interpretation of it, using characters of $\mathcal{N}=1$ for $D_4=SO(8)$, appearing as the transverse part of oscillators in the $10$-dimensional Lorentz group $SO(9, 1)$ under the RNS formalism and the GSO projection.

Another strong mathematical motivation that fundamental, high-energy physics exhibits supersymmetry is Deligne’s theorem on Tannakian reconstruction of tensor categories, when combined with Wigner’s classification of fundamental particles as irreducible, unitary representations of the Poincaré group. Indeed, this theorem is much more intuitive than the usual theorems that are being usually referred as motivation, namely Coleman-Mandula theorem and Haag-Lopuszanski-Sohnius theorem. Recall that, under Klein geometry (or under Cartan geometry if we talk about global spacetime models) the spacetime symmetry groups should be seen as more fundamental than spacetime itself. It is fun to observe that his “sub-exponential growth condition” is obvious under physical grounds. Deligne’s theorem does not state that spacetime symmetry groups need to have odd-supergraded components (they don’t).

What it does say though, is that the largest possible class of those groups that are sensible as local spacetime symmetry groups is precisely the class of algebraic super-groups. Or in other words, the class of algebraic super-groups precisely exhausts the moduli space of possible consistent local spacetime symmetry groups. This does not prove that fundamentally, local spacetime symmetry is a non-trivial supersymmetry. But it means that it is well motivated, at least mathematically, to expect that it might be one.

René Thom in the 1960s developed “catastrophe theory”, a branch of bifurcation theory in the field of dynamical systems with connections to singularity theory in geometry. Thom proposed that in 4-dimensions there are 7 different equilibrium surfaces and therefore, 7 possible “elementary catastrophes”: fold, cusp, shallowtail, butterfly, hyperbolic umbilic, elliptic umbilic and parabolic umbilic.

In his 1979 speech, into the prestigious Académie des Beaux-Arts of the Institut de France, Salvador Dalí described Thom’s theory of catastrophes as “the most beautiful aesthetic theory in the world“. In his first (and only) meeting with René Thom he recalled that Thom told him he was studying tectonic plates at the time.

Indeed, Dalí’s penultimate drawing in 1983 was given the title “The topological abduction of Europe”, with eminent seismic fractures in it, while the algebraic equation for the shallowtail appeared in the lower left corner:

His last painting, in May of 1983 was titled “The shallowtail”:

This provoked Dalí  to question him about the railway station at Perpignan in France (a city in south France near the Pyrénées) which happened to be a place of particular significance for the artist, having declared it to be the “centre cosmique de l’univers” in the 1963s after experiencing a vision of cosmogonic ecstasy there. Unfortunately, the place is mostly known the last decades from the serial killer case that took place between 1995-2001. Many art experts that period collaborated with police giving analytic reports in order to spot any patterns or potential links between the killings and Dali’s paintings.

The following two years draw a painting called “The mystic of the railway station of Perpignan”. Thom is reported to have replied, “I can assure you that Spain pivoted precisely -not just in the area of- but exactly there, where the Railway Station in Perpignan stands today”. Dalí was immediately enthralled by Thom’s statement, influencing his series “Série des catastrophes” above.

Actually, the full title of the work is pretty verbose: “Gala looking at Dalí in a state of anti-gravitation in his work of art “Pop-Op-Yes-Yes-Pompier” in which one can contemplate the two anguishing characters from Millet’s Angelus in the state of atavic hibernation standing out of a sky which can suddenly burst into a gigantic Maltese cross right in the heart of the Perpignan railway station where the whole universe must converge“.

As Dalí explains, the two characters on the opposite sides in the painting are taken from the famous “Angelus” painting of Jean-François Millet, where this time the fork (which in the original painting thrusts into the fertile ground) is associated with the bleeding wound of the pierced side of Christ’s sacrifice on the Cross, that can be seen in the center of the composition. Dalí himself appears twice on the painting, one at the top of it, with his arms spread and another one at the center floating in the vacuum. At the bottom, there is a calm sea and a boat, probably a symbol of the passage from life to death and along the golden ratio of the border line segment, there is “Gala contemplating” immobilized all those scenes that mirror the helplessness of man facing death and fading into nothingness. There is also a sex scene on the right coming out of nowhere, typical of surrealism. The flat wagon on the left stands as a reminder of the central theme of the painting which is the railway station.

Anyway, René Thom in his PhD thesis in 1951 under the supervision of Henri Cartan with title “Espaces fibrés en sphères et carrés de Steenrod“, proved (among other things) that in general, a homology cycle of a nonsingular compactification manifold cannot be represented by a nonsingular submanifold. Indeed, it turns out that dimension $6$ is the lowest such dimension in which a homology class may not be representable by a smooth manifold.

On the physical side of things, we now know that while in general the Freed-Witten anomaly is a necessary condition for the homology class of a $D$-brane to lift to a twisted K-theory class, the condition is also sufficient for all p-branes where $p \neq 6$ when the N-S $3$-form is topologically trivial. A brane wrapping a representable cycle carries a $K$-theory charge if and only if its Freed-Witten anomaly vanishes. Therefore, a brane wrapping a representable cycle carries a $K$-theory charge iff its Freed-Witten anomaly vanishes. But does this mean that $D$-branes can wrap such non-representable cycles? The framework of twisted $K$-theory that classifies R-R fields is indispensable here if we want to understand questions of that nature. Indeed, it turns out that some $K$-theory charges are only carried by branes that wrap non-representable cycles.

There is a very curious theorem by Shelah which states that:

If for every natural number $n$ we have $2^{\aleph_n} < \aleph_{\omega}$ then, $2^{\aleph_{\omega}} < \aleph_{\omega_4}$.

An other way to state this is this one: if $\aleph_{\omega}$ is a strong limit cardinal then: $$\prod_{n=0}^{\infty} \aleph_n < \aleph_{\omega_4} $$

It turns out that the only dimensions $n$ for which a sphere $S^n$ admits a unique differentiable structure are exactly $n=1, 2, 3, 5, 6, 12, 56, 61$.

In all other dimensions, except $n=4$, we get the existence of exotic spheres.

What happens at dimension $4$ is still largely unknown and it goes by the name of smooth Poincare conjecture, the only open case of generalized Poincare conjecture.

χαῖρε, ξεῖνε, παρ᾿ ἄμμι φιλήσεαι

Odys, a, 123

This blog will be mainly about mathematics, physics, philosophy, linguistics, history, poetry, art and theology.