René Thom in the 1960s developed “catastrophe theory”, a branch of bifurcation theory in the field of dynamical systems with connections to singularity theory in geometry. Thom proposed that in 4-dimensions there are 7 different equilibrium surfaces and therefore, 7 possible “elementary catastrophes”: fold, cusp, shallowtail, butterfly, hyperbolic umbilic, elliptic umbilic and parabolic umbilic.
In his 1979 speech, into the prestigious Académie des Beaux-Arts of the Institut de France, Salvador Dalí described Thom’s theory of catastrophes as “the most beautiful aesthetic theory in the world“. In his first (and only) meeting with René Thom he recalled that Thom told him he was studying tectonic plates at the time.
Indeed, Dalí’s penultimate drawing in 1983 was given the title “The topological abduction of Europe”, with eminent seismic fractures in it, while the algebraic equation for the shallowtail appeared in the lower left corner:
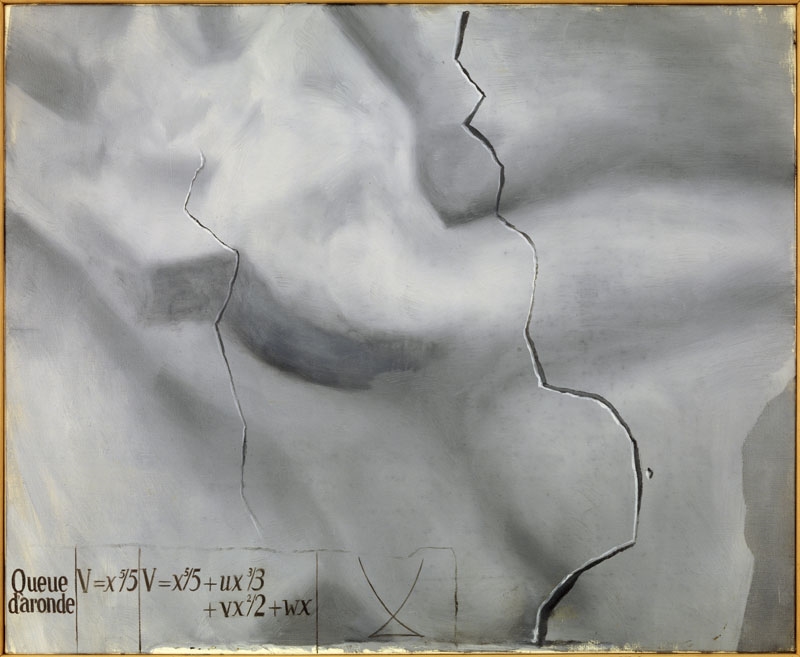
His last painting, in May of 1983 was titled “The shallowtail”:

This provoked Dalí to question him about the railway station at Perpignan in France (a city in south France near the Pyrénées) which happened to be a place of particular significance for the artist, having declared it to be the “centre cosmique de l’univers” in the 1963s after experiencing a vision of cosmogonic ecstasy there. Unfortunately, the place is mostly known the last decades from the serial killer case that took place between 1995-2001. Many art experts that period collaborated with police giving analytic reports in order to spot any patterns or potential links between the killings and Dali’s paintings.

The following two years draw a painting called “The mystic of the railway station of Perpignan”. Thom is reported to have replied, “I can assure you that Spain pivoted precisely -not just in the area of- but exactly there, where the Railway Station in Perpignan stands today”. Dalí was immediately enthralled by Thom’s statement, influencing his series “Série des catastrophes” above.

Actually, the full title of the work is pretty verbose: “Gala looking at Dalí in a state of anti-gravitation in his work of art “Pop-Op-Yes-Yes-Pompier” in which one can contemplate the two anguishing characters from Millet’s Angelus in the state of atavic hibernation standing out of a sky which can suddenly burst into a gigantic Maltese cross right in the heart of the Perpignan railway station where the whole universe must converge“.

As Dalí explains, the two characters on the opposite sides in the painting are taken from the famous “Angelus” painting of Jean-François Millet, where this time the fork (which in the original painting thrusts into the fertile ground) is associated with the bleeding wound of the pierced side of Christ’s sacrifice on the Cross, that can be seen in the center of the composition. Dalí himself appears twice on the painting, one at the top of it, with his arms spread and another one at the center floating in the vacuum. At the bottom, there is a calm sea and a boat, probably a symbol of the passage from life to death and along the golden ratio of the border line segment, there is “Gala contemplating” immobilized all those scenes that mirror the helplessness of man facing death and fading into nothingness. There is also a sex scene on the right coming out of nowhere, typical of surrealism. The flat wagon on the left stands as a reminder of the central theme of the painting which is the railway station.

Anyway, René Thom in his PhD thesis in 1951 under the supervision of Henri Cartan with title “Espaces fibrés en sphères et carrés de Steenrod“, proved (among other things) that in general, a homology cycle of a nonsingular compactification manifold cannot be represented by a nonsingular submanifold. Indeed, it turns out that dimension $6$ is the lowest such dimension in which a homology class may not be representable by a smooth manifold.
On the physical side of things, we now know that while in general the Freed-Witten anomaly is a necessary condition for the homology class of a $D$-brane to lift to a twisted K-theory class, the condition is also sufficient for all p-branes where $p \neq 6$ when the N-S $3$-form is topologically trivial. A brane wrapping a representable cycle carries a $K$-theory charge if and only if its Freed-Witten anomaly vanishes. Therefore, a brane wrapping a representable cycle carries a $K$-theory charge iff its Freed-Witten anomaly vanishes. But does this mean that $D$-branes can wrap such non-representable cycles? The framework of twisted $K$-theory that classifies R-R fields is indispensable here if we want to understand questions of that nature. Indeed, it turns out that some $K$-theory charges are only carried by branes that wrap non-representable cycles.
