
Είναι ευρέως γνωστό πως εκτός από την μυστηριώδη προσωπική σχέση που είχε ο αυτοδίδακτος Ραμανουτζάν με τους αριθμούς, είχε και μία ασυναγώνιστη ικανότητα για ταχύτατους υπολογισμούς. Χαρακτηριστικό παράδειγμα είναι η συνάντηση που είχε με τον Χάρντι, όταν ο τελευταίος τον επισκέφθηκε στο νοσοκομείο: προκειμένου να τον διασκεδάσει του ανέφερε πως το ταξί με το οποίο κατέφθασε στο νοσοκομείο είχε έναν πολύ βαρετό αριθμό, το $1729$. Ο Ραμανουτζάν γρήγορα τον διόρθωσε λέγοντας:
“Όχι, όχι, ο αριθμός αυτός έχει πολύ μεγάλο ενδιαφέρον καθώς είναι ο μικρότερος αριθμός ο οποίος δύναται να γραφτεί ως άθροισμα δύο κύβων με δύο διαφορετικούς τρόπους: $1729 = 1^3 + 12^3 = 9^3 + 10^3$”
Αριθμοί με ανάλογες ιδιότητες καλούνται σήμερα “αριθμοί των ταξί” λόγω αυτού του περιστατικού. Εκ πρώτης όψεως, ίσως φαίνεται υπερβολή να μελετήσει κάποιος τέτοιους αριθμούς περαιτέρω. Όπως όμως συμβαίνει συχνά στην Θεωρία Αριθμών, φαινομενικά απλές ιδιότητες φανερώνουν πολύ βαθιές αλγεβρο-γεωμετρικές δομές στο μαθηματικό σύμπαν. Πράγματι, τα τελευταία χρόνια οι αριθμοί αυτοί του Ραμανουτζάν βρίσκουν απρόσμενες εφαρμογές στις ιδιότητες των μελανών οπών και μας οδηγούν σε μια καλύτερη κατανόηση της φυσικής τους κοντά στον ορίζοντα γεγονότων ή στο λεγόμενο παράδοξο της πληροφορίας. Αλλά και οι υπόλοιπες εργασίες του Ραμανουτζάν φαίνεται να σχετίζονται με την κβαντική βαρύτητα, όπως για παράδειγμα τις επιφάνειες $K3$ που αποτελούν χαμηλότερης διάστασης ανάλογα των συμπαγοποιήσεων των εξωτικών διαστάσεων στη θεωρία χορδών και την κβαντική βαρύτητα.

Ένα παρόμοιο περιστατικό συνέβη ένα μεσημέρι στο σπίτι που μοιραζόταν με τον Ινδό ομογενή του και μετέπειτα διάσημο στατιστικολόγο Μαχαλανόμπις, την ώρα που ο Ραμανουτζάν βρισκόταν στην κουζίνα και μαγείρευε. Ο Μαχαλανόμπις του είπε πως διάβασε έναν γρίφο στην Βρετανική εφημερίδα Strand ο οποίος τον προβλημάτησε και είχε ως εξής:
Βρισκόμαστε σε μια οδό στην πόλη Λέβεν του Βελγίου στην οποία $n$ σπίτια είναι αριθμημένα με την σειρά $1, 2, 3, \dots, n$. Υπάρχει ένα σπίτι για το οποίο το άθροισμα των σπιτιών αριστερά του είναι το ίδιο με το άθροισμα των σπιτιών δεξιά του. Εάν το πλήθος των σπιτιών $n$ είναι ένας αριθμός μεταξύ του $50$ και του $500$, μπορείτε να βρείτε τι νούμερο έχει αυτό το μοναδικό σπίτι;
Ο Ραμανουτζάν σκέφτηκε για λίγα μόνο δευτερόλεπτα και έδωσε στιγμιαία την απάντηση. Ο Μαχαλανόμπις κατάπληκτος τον ρώτησε πως κατάφερε να βρει τη σωστή απάντηση τόσο γρήγορα και ο Ραμανουτζάν απάντησε:
«Είναι απλό. Όταν άκουσα το πρόβλημα, ήξερα πως η απάντηση θα είναι ένα συνεχές κλάσμα. Τότε αναρωτήθηκα: όμως ποιο συνεχές κλάσμα; Και τότε η απάντηση μου ήρθε στο μυαλό».
Το πρόβλημα μοιάζει απλό αλλά δεν είναι τόσο στοιχειώδες έτσι ώστε να μπορεί να επιλυθεί τόσο γρήγορα από οποιονδήποτε δυνατό λύτη. Αλλά πέρα από αυτό, η απάντηση του Ραμανουτζάν είναι ακόμα πιο ενδιαφέρουσα και σε ένα δεύτερο επίπεδο. Θυμηθείτε πως το πρόβλημα είναι διατυπωμένο με τέτοιο τρόπο έτσι ώστε να περιορίζει το εύρος των δυνατών λύσεων, καθώς περιορίζει το πλήθος των σπιτιών σε $50-500$. Ο Ραμανουτζάν βρίσκοντας ένα συνεχές κλάσμα ως απάντηση, στην πραγματικότητα αντί να βρει μία λύση στο πρόβλημα, βρίσκει όλες τις δυνατές λύσεις ταυτόχρονα! Στην παρούσα ανάρτηση θα ήθελα να προσπαθήσω να εξηγήσω πως μπορεί να φτάσει κανείς σε αυτή την γενικευμένη λύση. Τι είναι όμως ένα συνεχές κλάσμα;
Ένα συνεχές κλάσμα είναι μια μαθηματική έκφραση αποτελούμενη από μια επαναλαμβανόμενη διαδικασία ως εξής:

Παρατηρήστε πως αν αυτή η διαδικασία τελικά περατώνεται, τότε ο αριθμός του αποτελέσματος θα είναι υποχρεωτικά ρητός, ενώ αν όχι, ο αριθμός αυτός θα είναι εξ’ορισμού άρρητος (θυμηθείτε πως άρρητος είναι κάθε αριθμός που δεν είναι ρητός, δηλαδή κάθε αριθμός που δεν δύναται να γραφτεί ως λόγος δύο άλλων ακεραίων). Η ιστορία έχει ως εξής: η μυστικιστική σχολή των Πυθαγορείων δίδασκε πως κάθε αριθμός δύναται να γραφτεί ως ο λόγος δύο άλλων φυσικών αριθμών. Το δόγμα αυτό δεν ήταν αφηρημένο: σχετιζόταν με την γενικότερη φιλοσοφία και κοσμοθέαση που είχαν οι Πυθαγόρειοι σχετικά με την μουσική των ουρανίων σφαιρών, τη γεωμετρία, την ιερά τετρακτύ, την δωδεκαεδρική δομή του κόσμου, την πεμπτουσία και φυσικά το ίδιο το Πυθαγόρειο θεώρημα: $c^2 = a^2 + b^2$. Η ύπαρξη αρμονικών σχέσεων όπως $5^2 = 3^2 + 4^2$ που καλούνται Πυθαγόρειες τριάδες, ήταν αρκετές για να τους πείσουν για την μαθηματική κατανοησιμότητα του Σύμπαντος.

Μία ανεκδοτολική ιστορία λέει πως ένα ηλιόλουστο πρωϊνό όπου μια ομάδα μαθητών ταξίδευε προς την σχολή στον Κρότωνα, ο Ίππασος ο Μεταπόντιος είχε χαράξει στην κουπαστή με το ξίφος του ένα τετράγωνο με πλευρά ίση με $1$ και αναρωτιόταν ποιο είναι το μήκος της διαγωνίου σύμφωνα με το Πυθαγόρειο θεώρημα. Με άλλα λόγια, ποιος είναι εκείνος ο αριθμός που όταν τον πολλαπλασιάσω με τον εαυτό του να μου δώσει αποτέλεσμα $2$; Φανερά μπερδεμένος, φώναξε τον ίδιο τον Πυθαγόρα προκειμένου να του δείξει την κατασκευή και να τον βοηθήσει αλλά η παράδοση θέλει τον Πυθαγόρα να σκοτώνει (ή σε ευνοϊκότερα σενάρια να πετάει στη θάλασσα) τον Ίππασο μόλις αντιλήφθηκε σιωπηρά πως η θεωρία του δεν μπορεί να ευσταθεί.

Πράγματι λοιπόν, δεν υπάρχουν αριθμοί $p$ και $q$ έτσι ώστε $\frac{p^2}{q^2} =2$, το $\sqrt{2}$ είναι με άλλα λόγια, άρρητος. Σε αντίθεση με τους ρητούς αριθμούς, που είτε το δεκαδικό ανάπτυγμα τελειώνει (όπως το $\frac{1}{2}=0.5$) είτε είναι άπειρο αλλά επαναλαμβάνεται (όπως το $\frac{1}{3}=0.333…$), τα δεκαδικά ψηφία ενός άρρητου αριθμού δεν τελειώνουν ποτέ και μάλιστα η κατανομή των ψηφίων που ακολουθούν είναι “χαοτική” και ποτέ επαναλαμβανόμενη π.χ $\sqrt{2} = 1.41421356237…$. Αφού λοιπόν δεν μπορούμε να εκφράσουμε έναν άρρητο αριθμό, τίθεται με φυσικό τρόπο το ερώτημα πως μπορούμε τουλάχιστον να τον προσεγγίσουμε με μία ικανοποιητική προσέγγιση. Η έννοια των συνεχών κλασμάτων του Ραμανουτζάν προσφέρουν πράγματι μια τέτοια δυνατότητα. Για παράδειγμα γράφοντας το $\sqrt{2}$ ως $\sqrt{2} = 1 + (\sqrt{2} -1)$ και παρατηρώντας ότι: $(\sqrt{2} – 1)(\sqrt{2}+1) = 1$ μπορούμε να γράψουμε το $\sqrt{2}$ αναδρομικά:
| $\begin{align} \sqrt{2} &= 1+\frac{1}{1+\sqrt{2}} \\ &=1 + \frac{1}{2+\frac{1}{1+\sqrt{2}}} \\ &=1 + \frac{1}{2+\frac{1}{2+\frac{1}{1+\sqrt{2}}}} \\ &=1 + \frac{1}{2+\frac{1}{2+\frac{1}{2+\ldots }}} \end{align}$ |
η χρησιμοποιώντας ακόμα πιο οικονομική γραφή: $\sqrt{2} = [1; \bar{2}]$.
Το πρόβλημα των προσεγγίσεων των αρρήτων είχε ήδη απασχολήσει τους αρχαίους Έλληνες και φυσικά συνέχιζε να προβληματίζει και τους ανατολικούς Ρωμαίους όπως φαίνεται από την βαθιά μεταφυσική αρχιτεκτονική της Αγίας Σοφίας όπου κατά την τριχοτόμηση του Αριστοτέλη “τρεῖς ἂν εἶεν φιλοσοφίαι θεωρητικαί͵ μαθηματική͵ φυσική͵ θεολογική”, αντανακλά γνώση τόσο του προσεγγιστικού λόγου $\frac{22}{7}$ για τον αριθμό $\pi$ όπως χρησιμοποιήθηκε από την εξαντλητική μέθοδο του Αρχιμήδη αλλά και των μετέπειτα θεωριών του Ήρωνα του Αλεξανδρέα για το $\sqrt(2)$. Οι λόγοι αυτοί κατά κάποιο τρόπο επιλύουν το πρόβλημα μηχανικής που δημιουργείται από ένα αποδεδειγμένα αδύνατο μαθηματικό πρόβλημα όπως είναι ο τετραγωνισμός του κύκλου και κατ’αναλογία το αρχιτεκτονικό αποτύπωμα δίνει μια αίσθηση του αρρήτου του Θεού Λόγου και του μέγα μυστηρίου της Ενσαρκώσεως που υπερβαίνει πάσα φύση και πάσα έννοια.
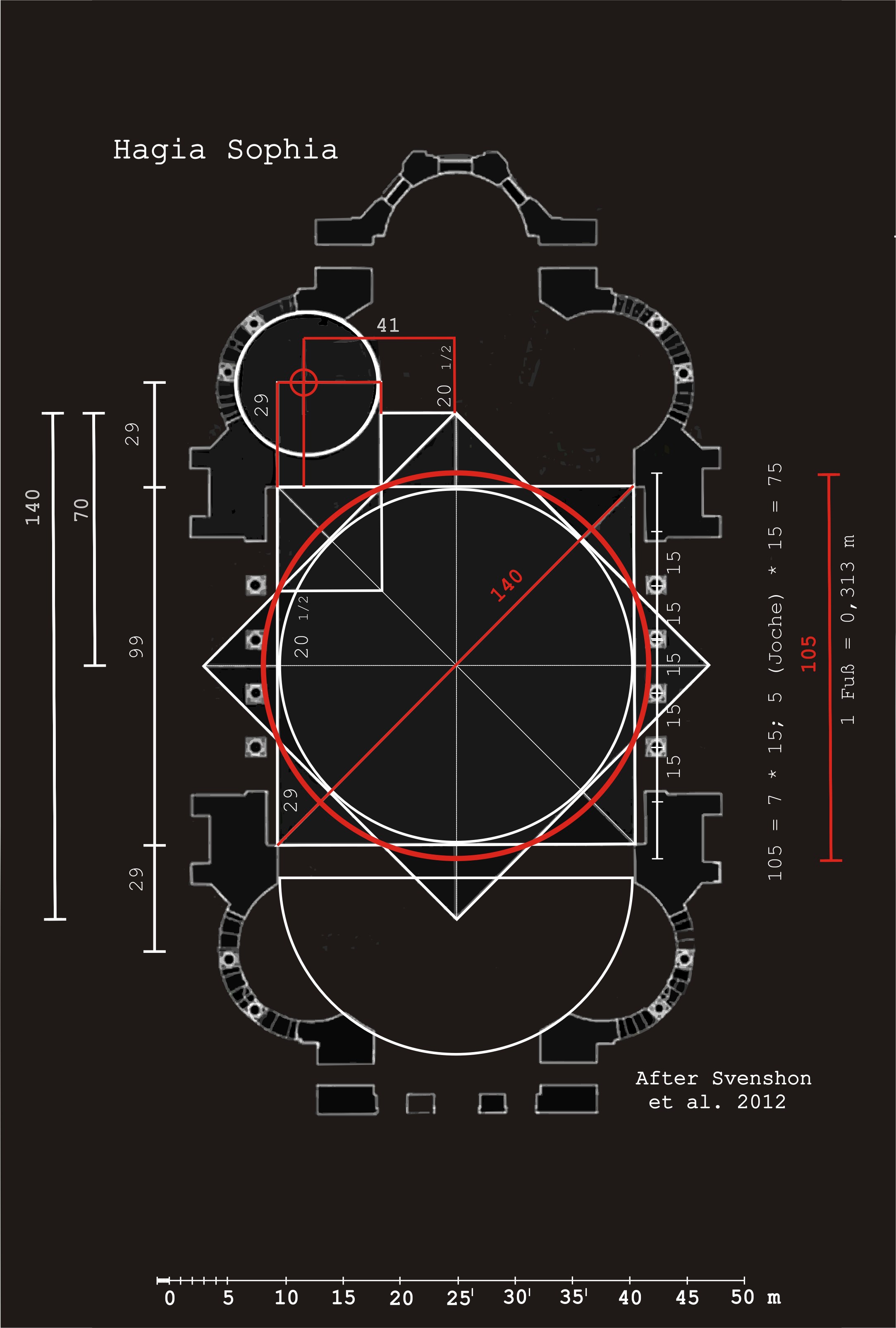
Έτσι, με σημερινούς όρους θα λέγαμε πως οι αρχαίοι Έλληνες υπολόγισαν διαδοχικές προσεγγίσεις, ολοένα μεγαλύτερης ακρίβειας, μέσω ενός συνεχούς κλάσματος για το $\sqrt{2}$, για παράδειγμα: $1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \frac{99}{70},\frac{239}{169},\frac{577}{408}$ κ.ο.κ. Πράγματι, αυτή η ακολουθία δίνει μια προσεγγιστική απάντηση για το μήκος της υποτείνουσας στο πρόβλημα του Ίππασου που αναφέρθηκε πιο πάνω.
Ας δούμε όμως τώρα τι σχέση έχουν όλα αυτά με τη λύση του Ραμανουτζάν. Έστω ότι υπάρχουν $n$ σπίτια και το σπίτι που αναζητούμε είναι το $z$. Δηλαδή,
$$1,2,3,\dots,z,z+1,z+2,\dots,…,n$$
Θέλουμε το άθροισμα αριστερά του $z$ να είναι το ίδιο με το άθροισμα δεξιά του, επομένως:
$$1+2+3+\dots+(z-1) = (z+1) + (z+2) + (z+3) + \dots + n$$
Άρα, από τον τύπο άθροισης για αριθμητικές προόδους θα έχουμε ότι:
$$\frac{z(z-1)}{2} = \frac{n(n+1)}{2} – \frac{z(z+1)}{2}$$
Δηλαδή,
$$z(z-1) = n(n+1) – z(z+1)$$.
Κάνοντας τις πράξεις, βρίσκουμε ισοδύναμα ότι:
$$8z^2 = (2n+1)^2 -1$$
Οπότε, θέτοντας $x=2n+1$ και $y=2z$ καταλήγουμε στην εξίσωση $x^2 – 2 y^2 = 1$ η οποία είναι γνωστή με το όνομα ενός άλλου Ινδού μαθηματικού που έζησε τον 7ο αιώνα, του Βραχμαγκούπτα. Σήμερα είναι γνωστή ως εξίσωση Pell και είναι υπεύθυνη για ολόκληρη την θεωρία των λεγόμενων πραγματικών τετραγωνικών επεκτάσεων $\mathbb{Q}(\sqrt{d})$. Αν αντικαταστήσουμε τις προσεγγίσεις που αναφέραμε πιο πάνω θα δούμε ότι η εξίσωση ικανοποιείται διαδοχικά:
$$3^2 – 2 \cdot 2^2 = 1$$
$$7^2 – 2 \cdot 5^2 = 1$$
$$17^2 – 2 \cdot 12^2 = 1$$
$$\dots$$
Επομένως, παίρνοντας για λύση της εξίσωσης Pell που μας ενδιαφέρει το συνεχές κλάσμα των διαδοχικών προσεγγίσεων του $\sqrt{2}$ θα έχουμε πράγματι ως λύσεις τα ζεύγη
$$(x,y): (3,2), (17,12), (99,70), (577,408), \dots$$
ενώ χρησιμοποιώντας τους αντίστροφους μετασχηματισμούς $n = \frac{x-1}{2}$ και $z = \frac{y}{2}$ τελικά παίρνουμε όλες τις δυνατές (άπειρες) λύσεις:
$$(n, z): (8, 6), (49, 35), (288, 204), \dots$$
Δεδομένου ότι η αρχική διατύπωση του προβλήματος περιείχε τον περιορισμό το $n$ να βρίσκεται μεταξύ $50-500$ η μόνη δυνατή απάντηση (η απάντηση που έδωσε ο Ραμανουτζάν στιγμιαία) είναι ότι το πλήθος των σπιτιών πρέπει να είναι συνολικά $288$ και το σπίτι έχει αριθμό $204$!
Πράγματι, μπορεί να ελέγξει κανείς ότι:
$$1+2+3+4+\dots+203 = 205+206+\dots+288 = 20706$$
Κατά παρόμοιο τρόπο, μπορεί κανείς να υπολογίσει την αμέσως επόμενη λύση, δηλαδή τον αριθμό του σπιτιού όταν το πλήθος των σπιτιών είναι μεγαλύτερο από $288$.
